準備
常微分方程式の初期値問題例: SIRモデル
総人口\(N\)人の閉じたコミュニティにおいて,伝染病が発生したとする。感染の強さを表わす伝達係数が\(r\),平均感染期間が\(1/a\)(日)とし,時刻\(t\)における感染者数を\(I(t)\),これから感染する可能性のある人数を\(S(t)\),伝染病が治ったか死亡した人数を\(R(t)\)とすると,必ず\(I(t) + S(t) + R(t) = N\)が成立する。
このとき,\(S(t), I(t), R(t)\)の導関数,すなわち,変化率は次のように決まっているものと考える。
- \(S'(t)\)は\(S(t)とI(t)\)の積に比例して減っていく。
- \(I'(t)\)は\(S(t)とI(t)\)の積に比例して増えるが,\(I(t)\)が多くなるとその分減少する。
- \(R'(t)\)は\(I(t)\)に比例して増えていく。
これを3次元の常微分方程式として表現すると下記のようになる。 \begin{equation} \frac{d}{dt}\left[\begin{array}{c} S \\ I \\ R \end{array}\right] = \left[\begin{array}{l} -r S I \\ r S I - a I \\ a I \end{array}\right] \label{eqn:sir} \end{equation} 初期条件:\(t_0 = 0\)として \[ [S(0)\ I(0)\ R(0)]^T = [S_0\ I_0\ R_0]^T \] とする。
SIRモデルの解導出とグラフ描画
"ode"フォルダを作成し,その中にtemplate.html,index.html,index.pyを作成すること。
template.html

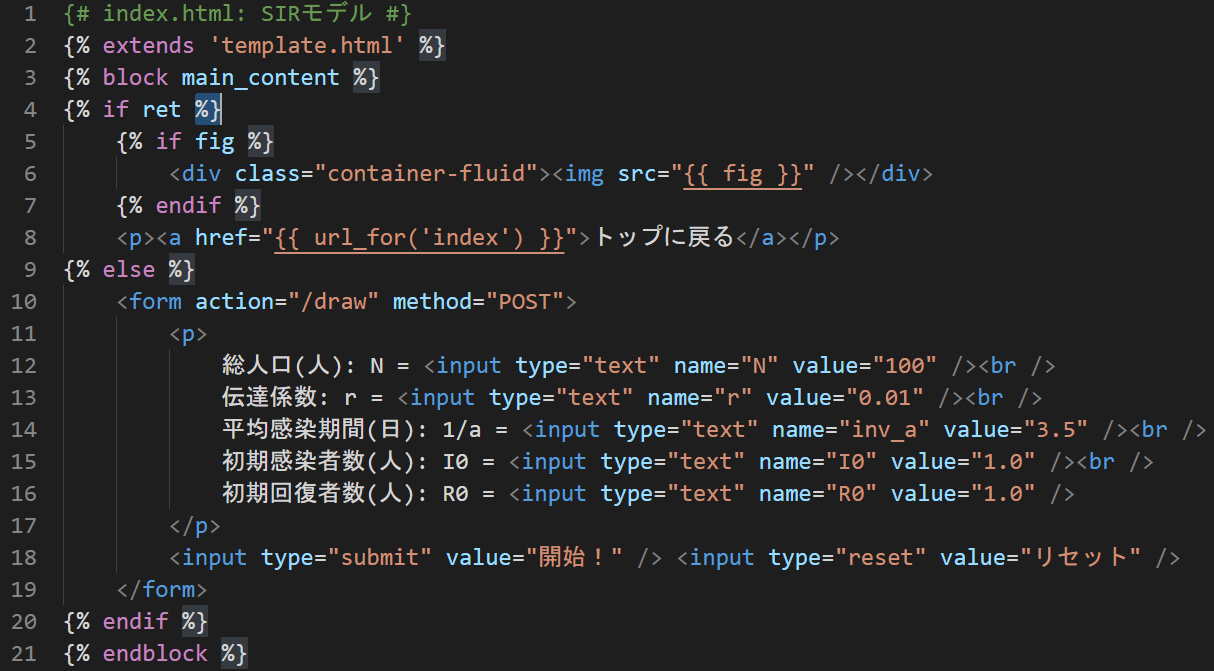
index.html
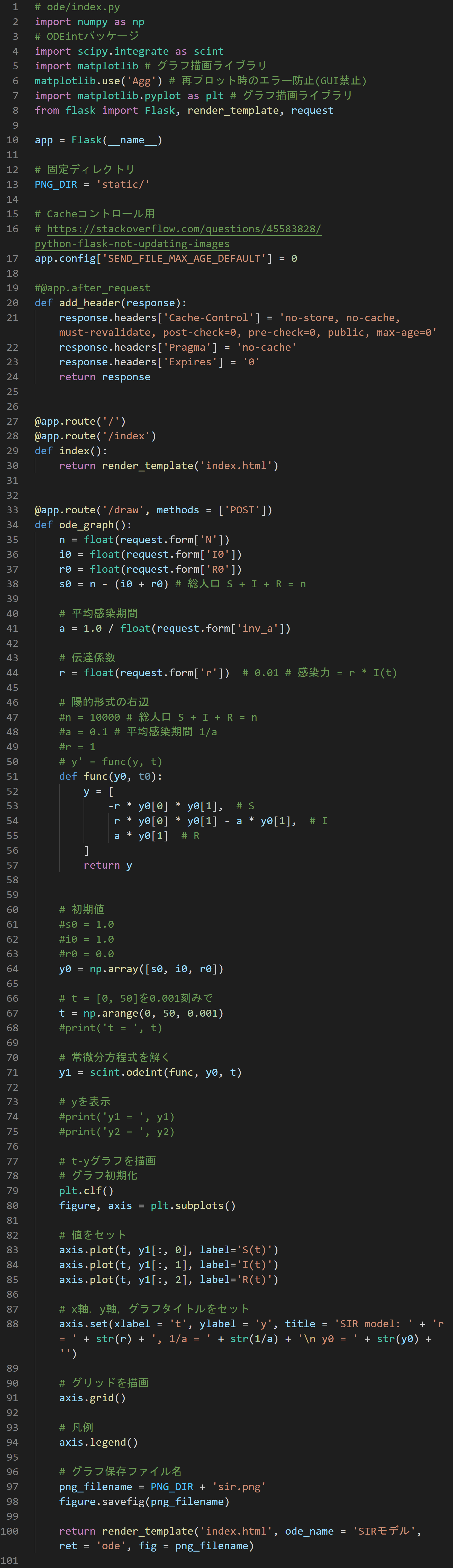
index.py
練習問題4
パラメータを次のように変化させた時の感染者数\(I(t)\)の変化について考察せよ。- \( 1/a \)が3の場合と14の場合
- \( r \)が0.01の場合と0.02の場合