準備
\(n\)変数の一次元関数\(u(x_1, x_2, ..., x_n)\)に対して \begin{equation} \phi\left(x_1, ..., x_n, u, \frac{\partial u}{\partial x_1}, ..., \frac{\partial^{i_1 + i_2 + \cdots + i_n} u}{\partial x_1^{i_1}\partial x_2^{i_2}\cdots\partial x_n^{i_n}}, ..., \frac{\partial^{i_1 + i_2 + \cdots + i_n} u}{\partial x_n^{i_1 + i_2 + \cdots + i_n}}\right)=0 \label{eqn:pde} \end{equation} となる関係式が成立する時,上式を\(i_1 + i_2 + \cdots + i_n\)階の偏微分方程式(Partial Differential Equation, PDE)\index{へんびぶんほうていしき@偏微分方程式}\index{partial differential equation}と呼び,関数\(u(x_1, x_2, ..., x_n)\)をこの偏微分方程式の解と呼ぶ。 偏微分方程式の数値解法には,(有限)差分法(Finit Difference Method, FDM)\index{さぶんほう@差分法}, 有限要素法(Finit Element Method, FEM), 境界要素法(Boundary Element Method, BEM)がある。このうち前者の2解法が,数値計算らしく,解析解が不明な場合でも有効である。 偏微分方程式の例としては2階線型偏微分方程式がよく取り上げられる。その一般式は \begin{equation} A(x, y))\frac{\partial^2 u}{\partial x^2} + B(x, y)\frac{\partial^2 u}{\partial x\partial y} + C(x, y)\frac{\partial^2 u}{\partial y^2} = F\left(x, y, u, \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}\right) \label{eqn:second_order_pde} \end{equation} と書ける。これを更に分類する方法として2次曲線の分類のアナロジーを用いる。即ち,ある領域\((x, y)\in D\subset\mathbb{R}^2\)において次の関係が成立する時,それぞれを次のように命名する。 \begin{eqnarray*} (B(x, y))^2 - 4A(x, y)C(x, y) > 0 &\Longleftrightarrow& \mbox{双曲型(Hyperbolic)} \\ (B(x, y))^2 - 4A(x, y)C(x, y) = 0 &\Longleftrightarrow& \mbox{放物型(Parabolic)} \\ (B(x, y))^2 - 4A(x, y)C(x, y) < 0 &\Longleftrightarrow& \mbox{楕円型(Elliptic)} \end{eqnarray*}
放物型の例:熱(伝導)方程式
\begin{equation} \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2} \label{eqn:heat_1dim} \end{equation} は,\(B(t, x) = 0\), \(A(t, x) = 0\), \(C(t, x) = 0\)より,放物型に分類される。これが平面\((x, y)\in\mathbb{R}^2\),および立体\((x, y, z)\in\mathbb{R}^3\)においてはそれぞれ \begin{eqnarray} \frac{\partial u}{\partial t} &=& \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\label{eqn:head_2dim} \\ \frac{\partial u}{\partial t} &=& \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}\label{eqn:heat_3dim} \end{eqnarray} となる。1次元熱方程式の差分法とPythonスクリプト
template.html

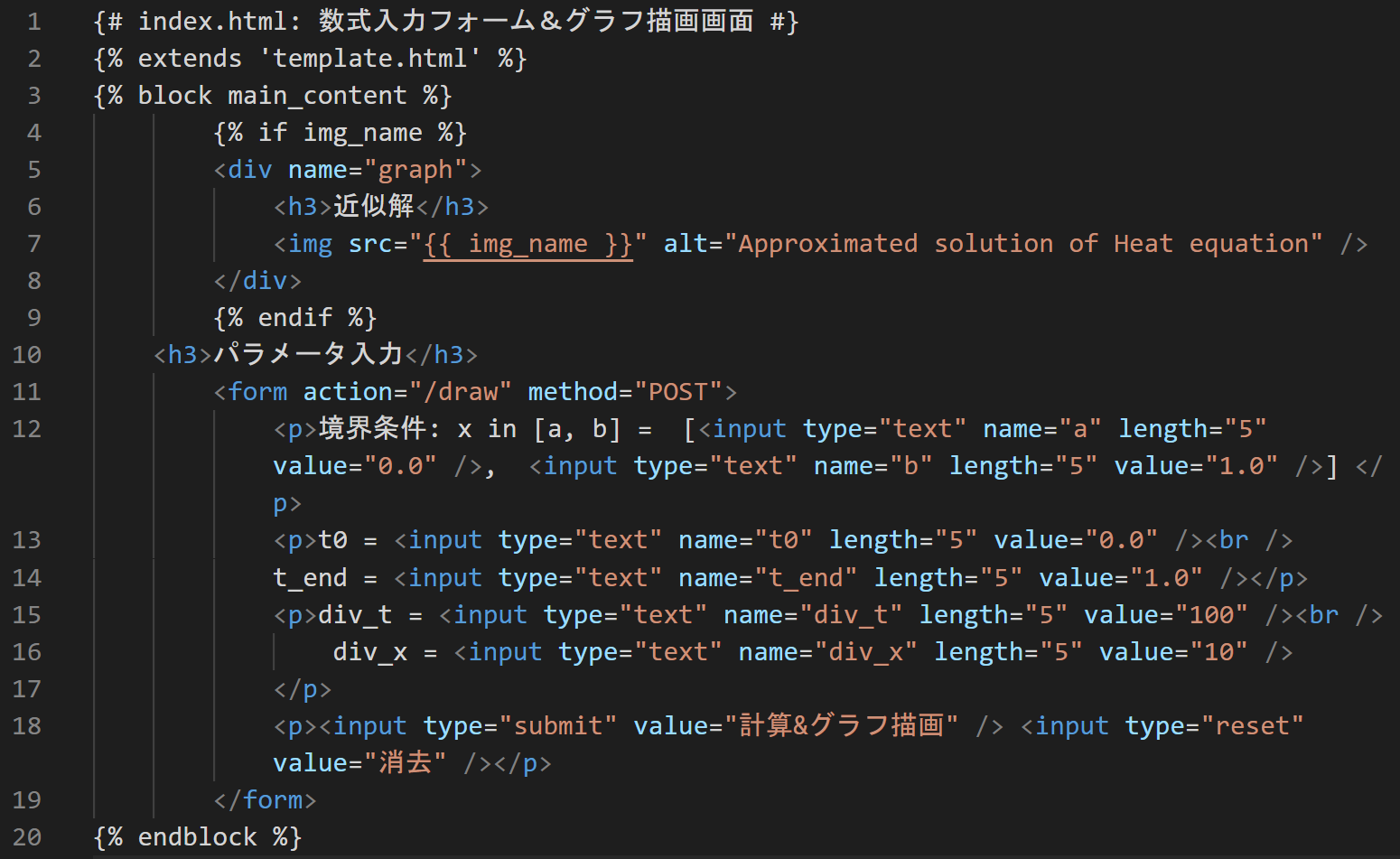
index.html
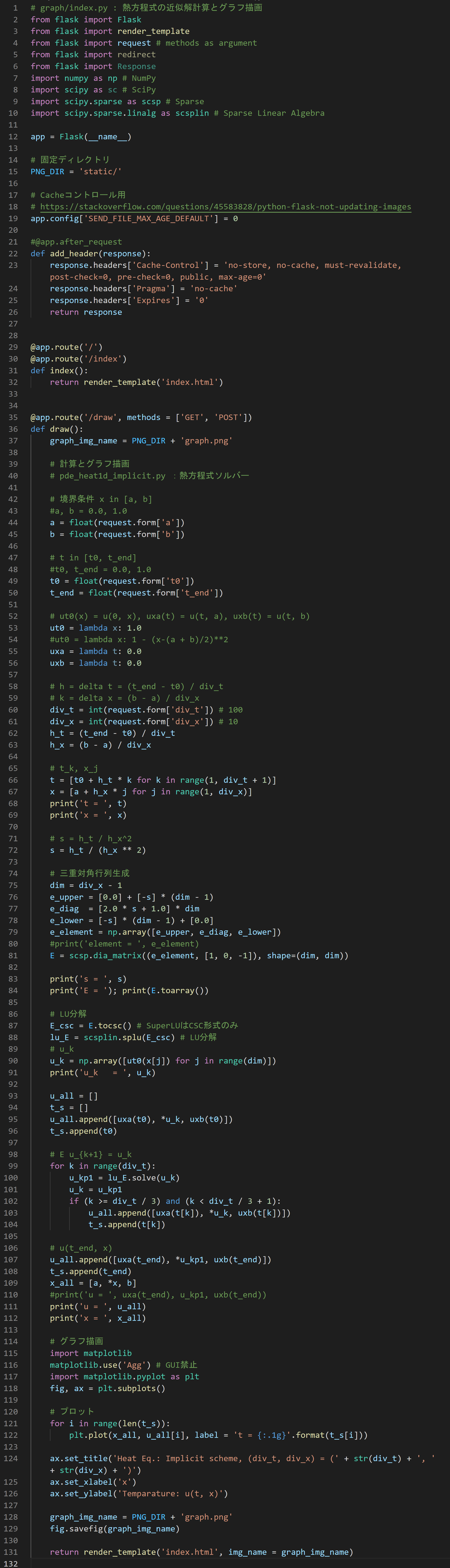
index.py
練習問題5
パラメータを次のように変化させた時の解\(u(t, x)\)の変化について考察せよ。- div_tの値が10の場合と100の場合
- 上記の各div_tに対し,div_xが10の場合と100の場合